Algebraic normal form
In Boolean logic, the algebraic normal form (ANF) is a method of standardizing and normalizing logical formulas. As a normal form, it can be used in automated theorem proving (ATP), but is more commonly used in the design of cryptographic random number generators, specifically linear feedback shift registers (LFSRs). A logical formula is considered to be in ANF if and only if it is a single algebraic sum (XOR) of a constant 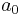 and one or more conjunctions of the function arguments. ANF is also known as "Zhegalkin polynomials" (Russian: полиномы Жегалкина) and as "Positive Polarity (or Parity) Reed-Muller" expression.
and one or more conjunctions of the function arguments. ANF is also known as "Zhegalkin polynomials" (Russian: полиномы Жегалкина) and as "Positive Polarity (or Parity) Reed-Muller" expression.
Putting a formula into ANF makes it easy to identify linear functions, as is needed for linear feedback in LFSRs: a linear function is one that is a sum of literals. Properties of nonlinear feedback shift registers can also be deduced from certain properties of the feedback function in ANF.
The general ANF can be written as:
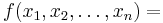 |
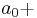 |
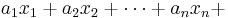 |
|
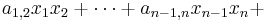 |
|
 |
|
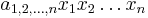 |
where 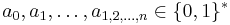 fully describes
fully describes  .
.
For each function  there is a unique ANF. There are only four functions with one argument:
there is a unique ANF. There are only four functions with one argument: 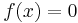 ,
, 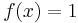 ,
, 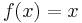 ,
, 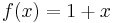 (all of them are given in the ANF). To represent a function with multiple arguments one can use the following equality:
(all of them are given in the ANF). To represent a function with multiple arguments one can use the following equality: 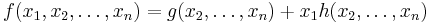 , where
, where 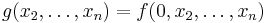 and
and  . Indeed, if
. Indeed, if 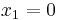 then
then 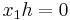 and so
and so  ; if
; if 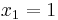 then
then 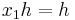 and so
and so 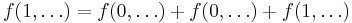 . Since both
. Since both  and
and  have less arguments than
have less arguments than  it follows that using this process recursively we will finish with functions with one variable. For example, let us construct ANF of
it follows that using this process recursively we will finish with functions with one variable. For example, let us construct ANF of 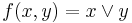 (logical or):
(logical or): 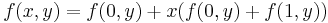 ; since
; since 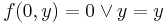 and
and 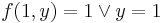 , it follows that
, it follows that 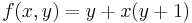 ; by opening the parentheses we get the final ANF:
; by opening the parentheses we get the final ANF: 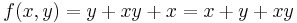 .
.